Die deskriptive Statistik und die Analyse mit Kreuztabellen sind identisch mit den nominalen Daten. Siehe dort...
Es gibt jedoch ein Testverfahren, wobei man die Rangordnung der Daten berücksichtigt.
Kurz erklärt: die einzelnen Gruppen werden gewichtet, am einfachsten aufsteigend von 1 bis 4, z.B. bei einer Einteilung einer Krankheit in 4 Stadien. Danach wird ein angepasster Chi-quadrat-Test angewandt. Der berechnete Chi-quadrat-Wert hat einen Freiheitsgrad.
Beispiel:
| Gruppe | 1 | 2 | 3 | 4 | 5 | 6 |
| Gewicht | 1 | 2 | 3 | 4 | 5 | 6 |
| Ereignis | 5 | 5 | 19 | 52 | 60 | 44 |
| Gesamtzahl | 6 | 12 | 30 | 99 | 126 | 106 |
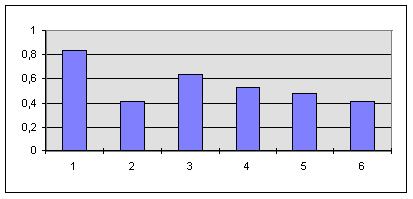
| Prozent | 0,83 | 0,42 | 0,63 | 0,53 | 0,48 | 0,42 |
Chi-quadrat 8,5193 d.f.= 5 p = 0,1298, nicht signifikant
Chi-quadrat für den Trend 5,40 d.f. = 1 p = 0,0201, signifikant.
Man sieht, dass die Prozentzahlen von links nach rechts über die Gruppen stetig abnehmen, abgesehen von einem "Durchhänger" in Gruppe 2. Dieser Trend ist eindeutig signifikant. Die Grafik zeigt es noch etwas besser.
